「解法のエウレカ」難易度や問題数、到達レベルは？使い方は？チャートと何が違う？一対一演習との差は？ⅢCは？大人気の問題集！

2025年3月26日

みなさん、こんにちは。
本日紹介する問題集はこちらです。

大人気問題集の「解法のエウレカ」です。

やっとⅡBが発売されまして、
これで
文系の人は使いやすくなりました。

ⅢCはいつ出版されるのでしょうか。
そもそも出版されるのでしょうか。
ⅢC も使ってみたいですね～

必要な人には
非常に役に立つ問題集です。

なぜ
この問題集は
大人気で役立つ問題集なのか
詳しく見ていきましょう！

どんな本なのか-内容・難易度

出版社：学研
著　者：竹内英人、小倉悠司
価　格：ⅠA：￥1,870、ⅡB：￥2,090
大きさ：B5判
発売日：ⅠA：2023年8月、ⅡB：2024年10月
厚　さ：ⅠA：264ページ、ⅡB：368ページ
色：3色刷り

まず
B5判なので
一般的な参考書問題集よりは
大判です。

厚さも結構あります。

ⅠAは
“緑”、赤、黒の3色刷りですが、
ⅡBは
“青”、赤、黒の3色刷りです。

構成

最初に「PIECE」で各単元の基本的な解法を確認します。
例題があり、”CHECK” として公式や定理、

そして、解く際に着目する点や解く流れなどが紹介されています。

その後
その知識を利用した解法が記載されています。

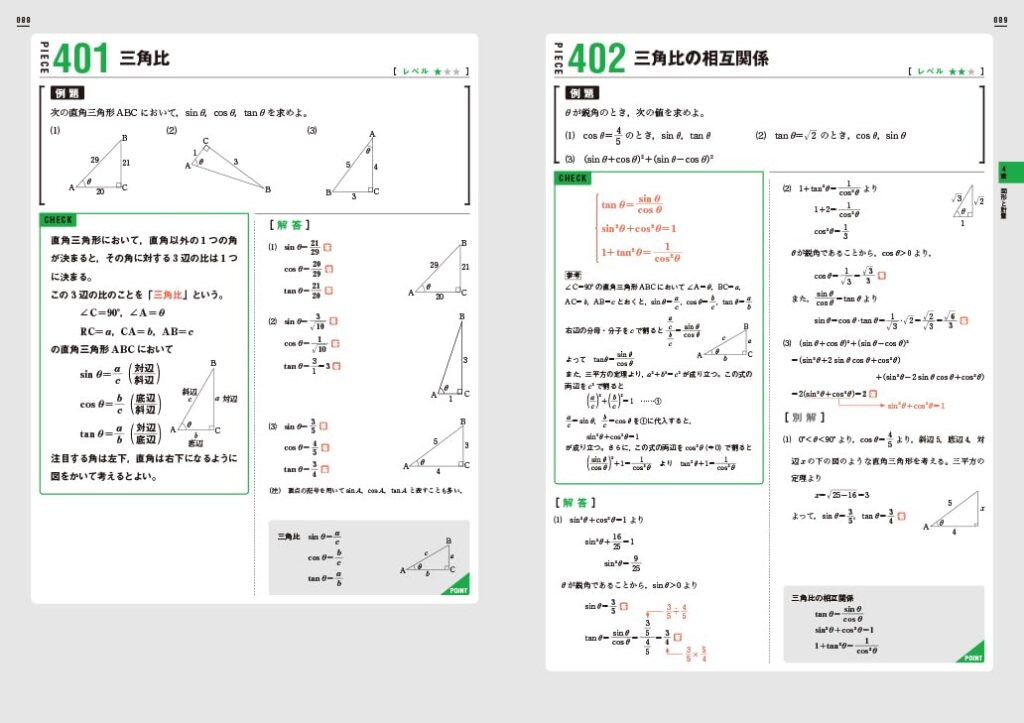
つづいて
「実践問題」になります。
ここでは
「PIECE」で確認した基本事項を利用して
教科書レベルから入試レベルに
対応するための問題演習を行います。

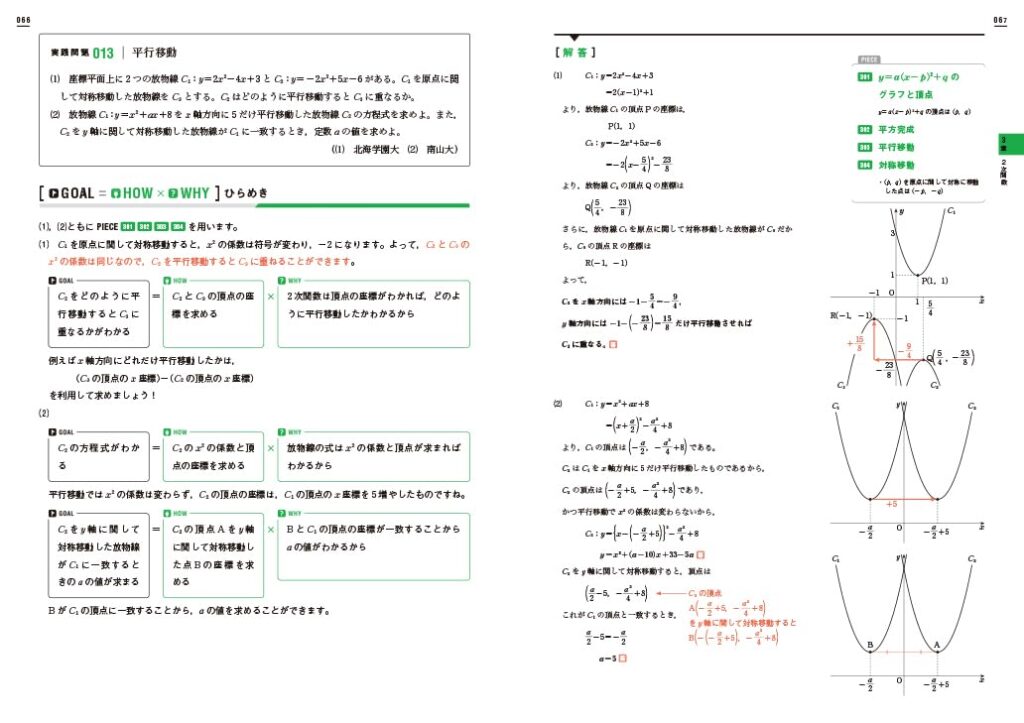
この「実践問題」の入試レベル問題では
“GOAL” に対して、
“HOW” と “WHY” がセットで示されております。
これらは
小問ごとに提示されています。

どう考えて
どのように解けば
解答に至るのかが分かりやすく説明されています。

なお、解く際に必要な知識である “PIECE” も記されています。

また、
ⅡB の巻末には
常用対数表と正規分布表が載っています。

問題数

ⅠA の PIECE の例題は、120題です。
実践問題は、75題です。

章	PIECE	実践問題
1章　数と式	10題	7題
2章　集合と論証	11題	5題
3章　2次関数	21題	11題
4章　図形と計量	14題	11題
5章　データの分析	9題	5題
6章　場合の数	16題	8題
7章　確率	11題	11題
8章　整数の性質	10題	10題
9章　図形の性質	18題	7題

ⅡB の PIECE の例題は、191題です。
実践問題は、83題です。

章	PIECE	実践問題
1章　いろいろな式	14題	10題
2章　図形と方程式	22題	10題
3章　三角関数	24題	9題
4章　指数関数・対数関数	20題	8題
5章　微分・積分	20題	10題
6章　数列	20題	17題
7章　ベクトル	34題	14題
8章　統計	37題	5題

問題レベル

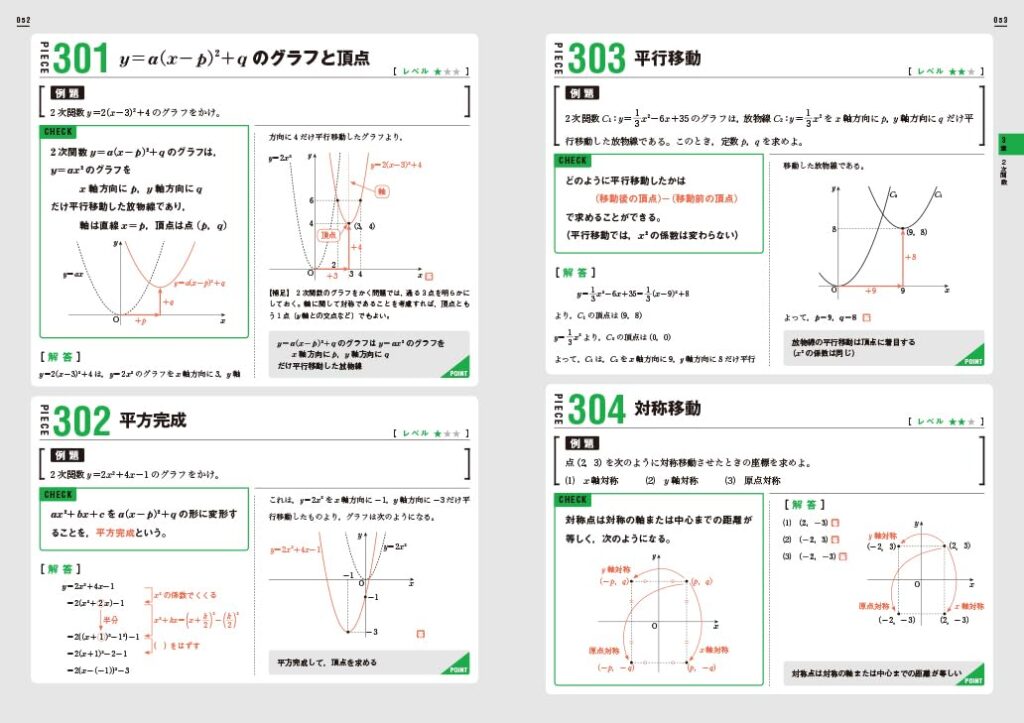
PIECE の例題には星でレベルが表示されています。
1～3の星で難易度を表しています。

問題は教科書に載っているレベルの問題です。
星3の問題は、
少し考える問題ではありますが
教科書レベルを超えるということはありません。

次の実践問題は
入試レベルの問題に対応できるようにするための
問題レベルです。

ほぼすべての問題が
入試過去問、または改題です。

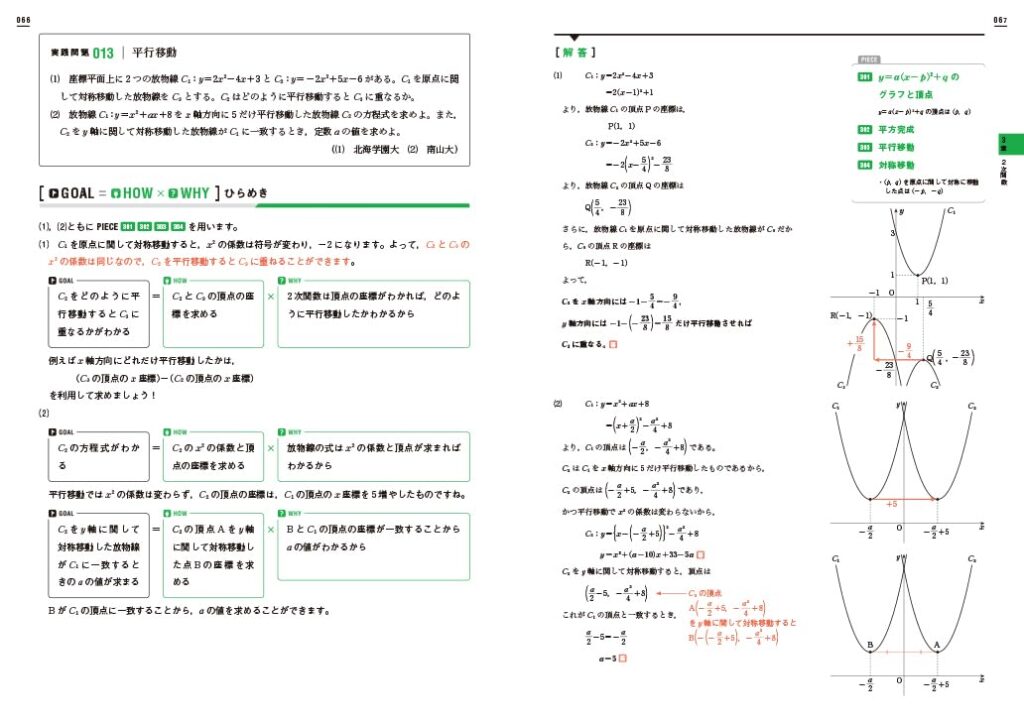
入試問題ではありますが難しいということはありません。
教科書レベルから入試レベルの橋渡しの役割をもつ
問題になっています。

基本知識や基本解法を身につけた人には
ちょうど良い問題です。

詳しさ

十分な解説です。

例題では
問題を解くために必要な知識や公式が紹介されており

その解答では
ときどき別解や参考情報の記載もあります。

基本的な知識を身につけた人であれば
理解のためにまったく問題ない説明です。

実践問題では
設問ごとに
どの “PIECE” を使って解くか、
さらに
“GOAL”、”HOW”、”WHY” の記載があり

問題に対して
どのように考えて解答していくかが示されており
「解答」として表されている内容に
納得することができます。

解答、説明に関しては
例題、実践問題ともに
十分な解説であると言えます。

使うべき人は誰か

教科書レベルの知識と解法を修得した人

本書は
大学入試に向けて
本格的に知識を活用した問題演習をスタートさせようとする人が
使用すると良いと思います。

“PIECE” は基本知識の公式や定理、考え方が記載されており
例題は教科書レベルです。

しかし
数学初学者が使用する問題集ではありません。
教科書の基本事項が網羅されているわけでもありません。

本書は
教科書レベル知識の確認整理と
その問題演習からスタートしています。
つまり
教科書の知識や基本解法については
理解し、修得しているという前提で
使用する問題集です。

以下のような問題集を学習し,
仕上がっている人が
取り組むべき問題集です。

この「文系の数学」は非常に良い問題集です。
傑作です。
ただ、姉妹書の「文系の数学(実戦力向上編)」は結構難しいです。

実戦力向上編は
ムズっ！となりますが
エウレカを橋渡し的役割にして
エウレカの学習後に実戦力向上編に取り組めば
スムーズに学習できると思います。

基本知識や基本解法を修得し
それらを使用して
入試問題に対して
どのようにアプローチするのかを
学ぶ問題集です。

本書の
帯に書かれていますが
初見の問題について
どうやって
その問題を紐解いて
自分の持っている知識を組合せて解くのか

ということにフォーカスした
内容になっています。

教科書レベルの知識は修得し、
入試応用レベルの問題演習に進むための
橋渡しとなる問題集です。

問題集のレベル帯としては
誰もが学習すべきレベルの問題集ですね。

学習方法・使い方

本書の最重要事項は
“GOAL”、”HOW”、”WHY” です。

どのように知識を組み合わせて
問題を解くためのアプローチ訓練ができることが
最大の特徴です。

収録されている問題の選択はとても良く
「なんだこの問題？」
「なんだこの解き方は？」
みたいな
ちょっとはずれた選題や解説は
ほぼありません。

そのため
この問題集の問題を
完全に解けるようにするだけでも
価値はあります。

でも
それだけでは
本書の価値に届きません。

問題を見て
“GOAL”、”HOW”、”WHY” を
再現できるように学習を繰り返します。

特に “WHY” をすり込みましょう！