初めから始める数学（通称：はじはじ）新課程や問題レベルは？問題数や改訂の違いは？使うべき人は？かんたん？解説は詳しいの？

2024年4月7日

みなさん、こんにちは。
今回紹介する問題集は、

マセマ出版社「初めから始める数学」です。
たくさんあります。笑

こちら
何度も改訂されています。

改訂によって
大きく変わるということはありません。
毎回の改訂で
練習問題が追加され、
改訂分はマセマ出版社HPに掲載されています。
なんという親切さ！

どんな本なのか

端的に言えば
「教科書内容理解のための参考書」です。
とにかく説明が丁寧です。
深堀しているわけではありませんが、とても丁寧です。

マセマ出版社
著者：馬場敬之
Ⅰ ￥1485　A ￥1276　Ⅱ ￥1496　B ￥1375　Ⅲpart1 ￥1122　Ⅲpart2 ￥1353
※改訂されているので少し値段が違うかもしれません。

6冊あります。
各冊のページ数はどれも250ページ前後、
A5版で一般的な問題集のサイズと言えます。

問題数

改訂によって問題数が増えますが
おおよそで示します。

Ⅰについて

範囲	数と式	集合論理	二次関数	図形と計量	データ分析
day	1～4	5～7	8～11	12～15	16～17
練習問題	10問程度	5問程度	10問程度	10問程度	5問程度

Aについて

範囲	場合の数と確立	整数の性質	図形の性質
day	1～6	7～9	10～14
練習問題	25問程度	15問程度	15問程度

Ⅱについて

範囲	方程式・式と証明	図形と方程式	三角関数	指数対数	微分積分
day	1～5	6～9	10～13	14～15	16～21
練習問題	15問程度	15問程度	10問程度	15問程度	30問程度

Bについて

範囲	平面ベクトル	空間ベクトル	数列	確率分布・統計
day	1～4	5～7	8～11	12～15
練習問題	10問程度	10問程度	15問程度	20問程度

Ⅲpart1について

範囲	複素数平面	式と曲線	関数	数列の極限
day	1～3	4～7	8～9	10～12
練習問題	15問程度	15問程度	10問程度	20問程度

Ⅲpart2について

範囲	関数の極限	微分法	微分法応用	積分法	積分法応用
day	1～4	5～7	8～10	11～12	13～15
練習問題	15問程度	10問程度	10問程度	10問程度	20問程度

練習問題は
1冊につき50～60題ほどです。普通の問題集に比べるとかなり少ない量です。

途中の式変形が省略なく書かれており
その注釈もあります。
丁寧に説明されているゆえ
紙面を使い、練習問題は少ないということです。

構成

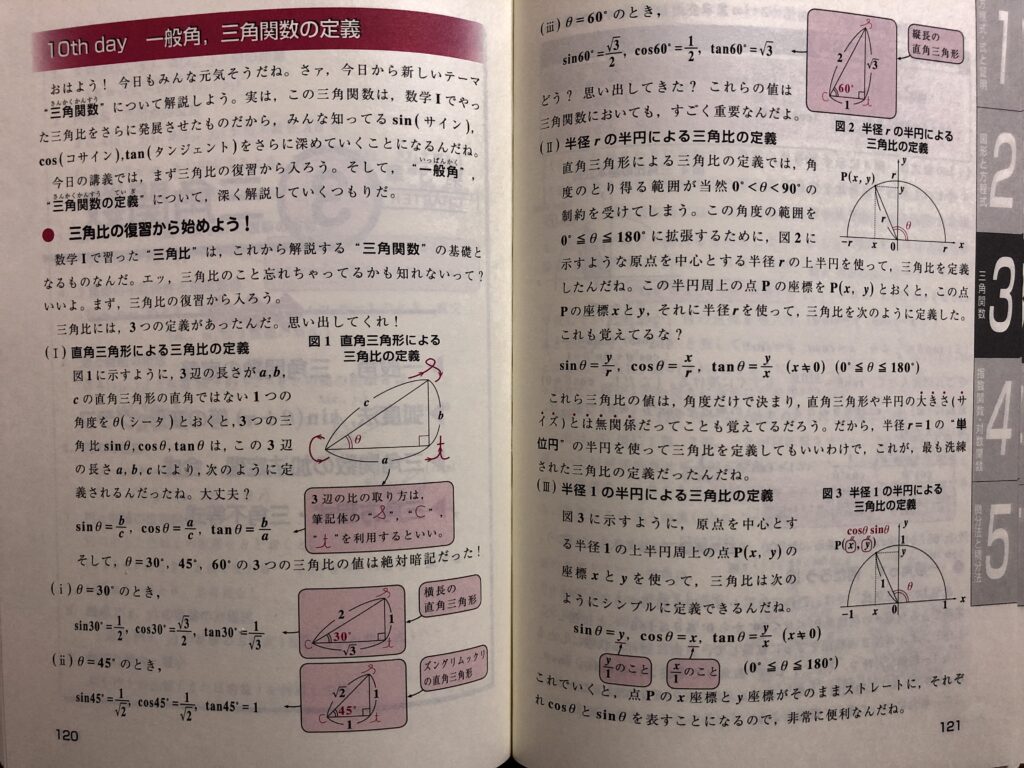
1つの単元が”day”で区切られています。
それは1日に進む目標となっていますが、
1つの”day”の学習時間は
60分～120分といったところです。
複数の”day”セクションを1日で終えることも可能です。

たとえば
Ⅲpart1の「関数」範囲は”8th day”と”9th day”の2セクションです。
2時間～4時間あれば、「関数」範囲は終えることができるということです。

それぞれの”day”の構成は以下のようになっています。

1.【教科書よりも丁寧な解説】
※公式、性質、重要事項などの紹介と解説
2.【練習問題】
3.【練習問題の解説・解答】
※注意事項や式変形の補足、図示
4.【公式エッセンス】（範囲最後のページで公式のまとめ）

このように
大変丁寧に説明されています。
網羅系参考書の解説でよく起こる
「どうして式がいきなりこれになっているの？？」
みたいなことがほとんどありません。

練習問題は本文の途中にあります。
問題と解答解説の分冊ではありません。

使うべき人は誰か

数学が本当に苦手で教科書理解ができていない人

とにかく平易な解説で一貫しています。
口語調の文章で
著者の「数学に親しんでもらいたい」という気持ちが
伝わってくる説明になっています。

基本事項を丁寧に
教科書よりもわかりやすく解説をされています。
計算の途中過程もとばすことなく記載されています。
どのように変化や計算させているのかを注によって豊富に示されてもいます。

ただ、丁寧ゆえ文章量が多く
それを読み進めていくことになります。

つまり
「読む」という覚悟は必要です。

それをクドいと感じる人もいるでしょう。

授業の予習をしたい人

教科書よりも丁寧に説明されているということは
この本を利用して
独学も十分に可能であるということです。

基本的に知識0からの教科書による予習や独学は
多くのエネルギーを使用します。
読解に時間がかかり、理解が不十分なところも点在します。

「初めから始める数学」シリーズは
丁寧にわかりやすく
とばすことなく解説されています。
これから新たに数学を学習しようという人、
または
基本から学習し直そうという人には
適した参考書・問題集であると言えます。

学習方法

この本は
教科書理解の助っ人的参考書です。
この本の内容が固まっていなければ
次の段階、
つまり基本解法の修得学習に進んだとしても効率が悪く
その学習の理解も十分とは言えず
大きな伸びも期待できません。

「初めから始める」シリーズの
説明の完全理解と練習問題の瞬解が目標です。
練習問題はかなり絞られています。
教科書に掲載されている問題と比べても
簡単なレベルに抑えてあります。

知識定着のためには
練習問題を追加する必要があります。
追加問題は教科書でも構いませんし、
同レベルの問題集でも構いません。

初めから解けるシリーズ　（初めから始めるシリーズの問題集）

マセマ出版社より
演習用の教材も出版されています。

学習時間との相談だとは思いますが
このレベルの基本問題は完璧に解けるようにしておきたいところです。

さて本書は
先ほど説明しましたが

”day”という項目で区切られています。

写真のように
第1章は項目通り進めば4日間で終えられるということです。
項目の数により
数学Ⅰの全範囲は17日間で通すことが可能です。
※上記「問題数」参照

この”1 day” 分は、1,2時間で学習できます。
1日に2～3 ”day” 分進むこともできますので
より短期間で1冊を終えられます。

受験生であれば
1週間で1冊を通し、
練習問題を中心に繰り返し
理解の下、瞬間で解けるようにしましょう。
2週間程度でパーフェクトにしたいですね。
それぐらいの気概は持って学習すべきです。

到達レベル

教科書レベルの基本知識・基本問題解法の修得

この本は
「教科書知識の理解助っ人」参考書です。
練習問題数も教科書の問題数より少なく
基本から標準の問題に絞ってあります。
基本的な問題をスラスラと解けるようにするためには
さらに演習が必要です。
教科書とか
「初めから解ける」シリーズとかで。

ただ
指導者がいるのであれば
「初めから始める」→【基本解法修得学習】
という感じで
演習をカットして次の段階に進むことも可能です。

塾では
そのように進んでいる生徒もいます。

たとえば
「初めから始める」→「基礎問題精講」のように。

基礎問題精講学習時には
少々質問が出てきます。

質問できる環境にあるのならば
このように進んでも
なんとかなります。

ただし
基礎問題精講の網羅性は高くはありません。
最低限でしのぐという場合に。

さらに厳選された問題数で
入試数学を乗り越える作戦もあります。

「初めから始める」の学習後に
このシリーズでも良いと思います。
収録問題が上質で丁寧に解説されています。
大変素晴らしい本です。

ⅠAⅡBの範囲だけで良いのなら
この本に接続することも良い選択です。

「数学は共通テストだけ」とか
「そんなに高いレベルまで不要」とか

もし、
そんな到達ラインを考えているのであれば
「初めから始める」の完成のあとに
「やさしい高校数学」もいいかもしれません。

共通テストも難しくなっていますので
共通テストだけと言っても
演習は重要です。

数学の学力を向上させるうえで
教科書内容の理解、基本知識の修得や基本問題が解けることというのは
絶対に必要なことです。
ここが固まっていなくては先に進めません。
進んだとしても伸びがやってきません。
苦しい数学がずっと続いてしまいます。

教科書理解の「助っ人」がほしいとき
是非この本を頼ってみてください。