みなさん、こんにちは。
今回紹介する参考書は、
旺文社「数学 入門問題精講」です。
名作です、この本は。
やっと数学ⅢCが発売され
数学ⅠA、ⅡB、ⅢCがすべてそろいました。
最新の改訂版のものを購入してください。
改訂前のものは
範囲をすべて網羅していないので。
旺文社の問題精講シリーズは
どの科目も
どのレベルも
よく仕上がっていると思います。
ただ
この「数学 入門問題精講」は
他の精講シリーズとは一味違います。
その理由を
本書を詳しく見ていきながら
説明したいと思います。

どんな本なのか
「数学初学者用であり、用語・概念説明が丁寧な教科書理解本」
という形容があっている本です。
出版社:旺文社
著 者:池田 洋介
価 格:ⅠA ¥1,320、ⅡB ¥1,430、ⅢC ¥1,540
大きさ:A5判
厚 さ:ⅠA 360ページ、ⅡB 392ページ、 ⅢC 448ページ
色:2色刷り
改訂前の入門問題精講ですけれど。

厚さなんて
どうでも良いかなとも思いますが
一応載せておきます。
結構な厚みを感じます。
基礎問題精講 数学よりは厚いです。
演習教材ではありませんので
問題&解説一体型になっています。
問題数
改訂前のものです。
(※改訂版ではありません)
【ⅠA】
| 章 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 単元 | 数と式 | 関数と 関数のグラフ | 三角比 | 場合の数 | 確率 | データの 分析 | 集合と論理 |
| 練習問題 | 14 | 15 | 12 | 11 | 11 | 6 | 6 |
| 応用問題 | 1 | 2 | 4 | 5 | 1 | 0 | 0 |
【ⅡB】
| 章 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 単元 | 式と証明 | 複素数と 方程式 | 図形と 方程式 | 三角関数 | 指数・ 対数関数 | 微分積分 | 数列 | ベクトル |
| 練習問題 | 9 | 10 | 18 | 12 | 18 | 19 | 12 | 20 |
| 応用問題 | 0 | 1 | 1 | 7 | 1 | 6 | 6 | 2 |
【Ⅲ】
| 章 | 1 | 2 | 3 | 4 | 5 | 6 |
| 単元 | いろいろな 関数 | 数列の 極限 | 関数の 極限と微分 | いろいろな 関数の微分 | 微分法の 応用 | 積分法 |
| 練習問題 | 7 | 11 | 12 | 9 | 14 | 21 |
| 応用問題 | 0 | 1 | 0 | 1 | 3 | 3 |
| 章 | 7 | 8 | 9 |
| 単元 | 積分法の 応用 | いろいろな 曲線 | 複素数平面 |
| 練習問題 | 12 | 8 | 13 |
| 応用問題 | 3 | 2 | 4 |
「練習問題」は検定教科書の例題や練習問題レベルで、
「応用問題」は章末問題レベルです。
基本的に「練習問題」「応用問題」は教科書内の問題レベルで
構成されています。
「応用問題」の中には
入試問題対策に突入していくための
基本解法レベルの問題もあります。
また
本書の導入部分の講義パートの説明のために
「例題」が載っていることがあります。
問題数からわかる通り
教科書よりも問題数は絞られています。
選ばれた問題です。
レベル
この本は
”問題演習を通して数学の問題を解けるようになろう”
というものではなく
あくまでも
「数学の土台を理解し固める」というものです。
そのためのの”掲載されている問題”なのです。
基礎知識を固める問題、
つまり
問題のレベルは教科書に掲載されているレベルのものです。
それ以上のものはありません。
得点を伸ばすための学習観点からすると
本書の学習後は
演習段階に進む必要がありますし、
本書問題数からすると
その演習は必須です。
構成

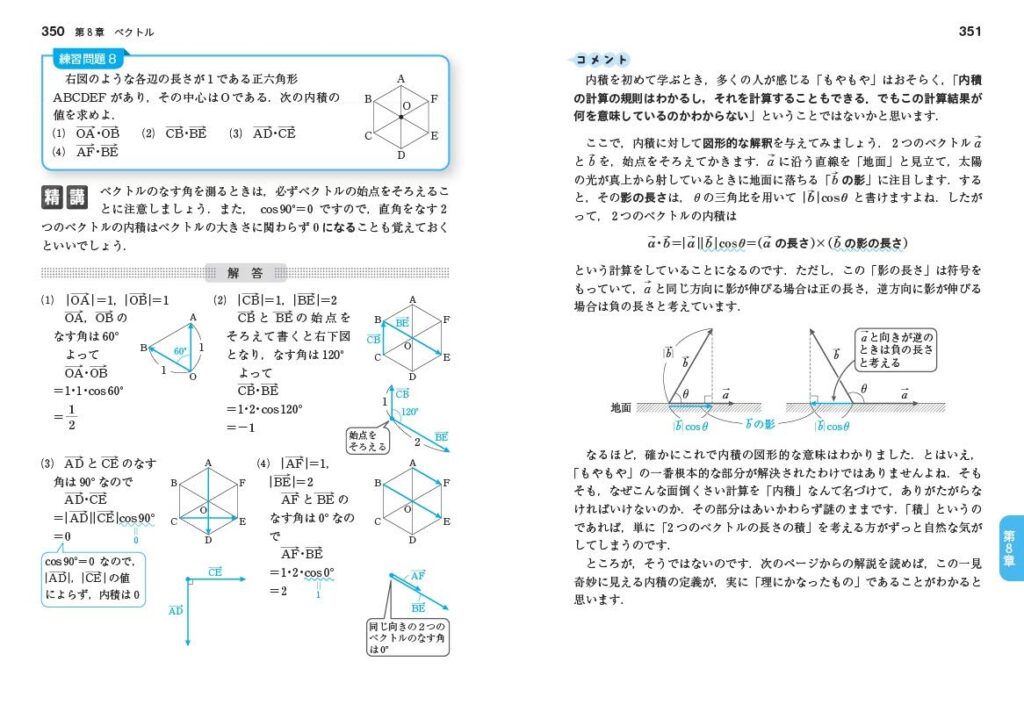
本書の大まかな流れは
〔導入・知識説明〕〔問題〕〔精講〕〔解答解説〕〔コメント〕
というものです。
この本の最大の特徴は
〔導入・知識説明〕の講義部分です。
詳しく説明されており
そして本質的です。
公式の証明も載っており、
どのように考えるのか、
何を理解しなければいけないのか、
なぜそうなるのか、
といったことが丁寧に書かれています。
教科書よりも詳しく丁寧に
そして
市販問題集ではありますが、
数学的に正しく記述されています。
〔精講〕では問題を解くうえでの方針や注意点が書かれています。
〔解答解説〕は丁寧です。計算過程も詳細に記載されています。

〔コメント〕や
ときどき出てくる〔コラム〕では
原則にしたがって
結果がどのように論理的に成立しているのかなどが
説明されており
大変ためになり、納得します。
素晴らしい内容になっています。
使うべき人は誰か
教科書を理解したい人
教科書を理解できれば
その後の数学学習は段階的にうまく進んでいくと思います。
ただ
教科書を理解するということが
案外難しいのです。
授業に使用する教材が教科書であり
先生の授業があるという前提のものです。
そういう点で
独学で「教科書を理解せよ」ということに
「力技だな」と思うこともあります。
もちろん教科書を理解できるのであれば
何も問題ありませんので
そのまま学習を進めていけば良いのです。
躓きがある人にとっては
学習の「良きパートナー」となるような教材が
本書です。
学校の授業についていけない人の手助けになってくれる本です。
この本は
数学を”撫でる”ようなぬるさはありません。
口語調で親しみやすさがあるわけではありません。
だからと言って
冷たく突き放した説明かと言えば
まったくそんなことはなく
とっても丁寧に解説されています。
著者の池田先生の素晴らしさを感じます。
なんとなくではなく
なぜそれが成立するのか
真正面から数学的に正確に記述しています。
理解するのに十分な詳しさと丁寧さを持っており
本書で数学的な正しさに触れることは
後の数学学習で
大きな意味を持つのだと思います。
「土台のための本」なのです。
授業の予習をしたい人
中学までの数学の理解ができているならば
高校に入学して
先取りとして
本書を使用することが可能です。
中学内容が完成している中学生もこの本で学習可能です。
「ここは難しいな」と感じるところがあったり
完璧理解に至らないところもあるかもしれません。
そこは、それで構いません。
学校の授業を受けたり
本書を復習したり
または
先に進むことによって
理解が醸成されるということもあります。
予習という使用方法なのであれば
7割程度の理解で十分なので
まず全体像を把握することに重きを置くと良いと思います。
そのことは
「はじめに」で著者の池田先生も書いています。
基礎が固まっていない人
問題演習をしているのに
その学習内容に見合った得点や学力になっていない場合や
演習教材の解答解説が理解できない場合、
基礎事項の知識抜けが考えられます。
丸暗記に近い状態で
基本解法の暗記や
問題演習を続けていても
学力が理想的に向上することはありません。
使っている式の
「意味」を知ることや理解することが
向上のために不可欠なことです。
本質的な理解が本書で得られ、
不足していたピースがはまり、
大きく飛躍するきっかけになるかもしれません。
学習方法
教科書の内容を
教科書の代わりに本書使って理解定着させることが目標です。
最終的には
すべての理解が必要です。
講義部分の理解、
公式導出の理解、
問題の完全正解と解説の理解、
この本の内容が
今後の数学学習の土台であることを考えると
どの部分も粗末に扱うことはできません。
問題だけ解ければよいという本ではなく、
より重要な箇所は
講義や解説、コラムやコメントなどの
説明の部分です。
ここを血肉化することが
この本を学習する価値です。
とは言っても
「その結果に至るための考え方」がしっかりと書いてあるので
数学がとにかく、もう本当に、とっても嫌いという人には
苦しい本かもしれません。
公式の証明なんて吐いちゃうかもしれません。
ですから
はじめから完璧を目指すのではなく
どうしても
ひっかかる箇所があったとして
その部分は一旦「わからない」と保管し
先に進んでみることが
結構大切な学習方針ではないかと思います。
進むことによって
情報が整理され
理解に達しなかったところが
後に
わかるようになることはよくあることです。
わからない、ということを恐れずに。
そのことは
著者の池田洋介先生も言っています。
数学的に誤魔化しがないゆえに
難しいと感じることもあるかもしれませんが
正確に真正面からぶつかるということは
重要なスタートであり、
こんな本を求めている人は
かなり多いのではないかと思います。
入門問題精講が厳しいと感じる人は
以下の本を検討してみてはどうでしょうか。
同レベルです。

ちょっとタイプは違いますが
こちらも使えると思います。

これらは
入門問題精講よりは硬さがなく
取り組みやすさを感じるのではないでしょうか。
ただし
深みは入門問題精講の方が上です。
しっかりと数学を学べます。
将来
難関大学に挑戦する場合は
確固たる”礎” が必要です。
難関大学志望者は
是非本書を検討してください。
到達レベル
教科書の知識理解と定着・基本問題の解法理解
掲載されている問題は
教科書の例題、練習問題、章末問題レベルです。
入門問題精講が仕上がったとき
教科書の内容が入力されたということです。
ここが本書の到達ラインです。
しかも
本書で学習することで
将来的にハイレベルなところまで通用するような
基礎が固まります。
土台完成の必要性は
難度の高い問題を解けば解くほど
痛感します。
公式の導出、式の意味など
より深く理解できているということであり
これ以降の問題演習をスムーズに進めることができて
次の段階の
学習に綺麗につなぐことができると思います。
本書の完了後
共通テスト対策や過去問演習といった段階に
進めないことはないですが
かなり粗いステップですので
まずは
レベルを合わせた問題演習を行うことが良いと思います。
例えば
基礎問題精講とかですね。

基礎問題精講は悪くありませんが
問題や解説のレベルから
入門問題精講卒業者が学習すると
結構、質問が出ます。
質問できる環境であれば良いと思います。
この本も大変おすすめです。
問題が厳選されている素晴らしい問題集です。
丁寧な解説を望むのであればこちらの方が良いです。


チャートでゴリゴリ解法インプット!
みたいな学習も
まあ、できます。
それが好きなら。
ⅠAⅡBだけで良いのなら
典型問題解法のインプットと
入試標準問題の演習までできる
この問題集もオススメです。
チャートよりも問題は厳選されていますので
効率的です。

とにかく
入門問題精講の完成のあとは
一般的な
数学受験勉強に入っていけます。
入門問題精講、良い本です。
是非是非
本書を手に取り、
見てみてください。
–※新課程と旧課程にご注意ください–
【新課程バージョン】
改訂版!!(整数も載っています!!)
【旧課程バージョン】






